插入 Latex 数学公式

说明

本编辑器使用的是性能更佳的 Katex 作为数学公式解析引擎。

撰写数学公式时，有三种方式：

1. 行内模式
2. 单行模式
3. 代码块模式

如下

1. 行内模式 行内的公式 $$E=mc^2$$ 行内的公式，行内的$$E=mc^2$$公式。

将会被解析为：

行内的公式 E=mc^2 行内的公式，行内的E=mc^2公式。

2. 单行模式

一整行都是数学公式的情况下，如：

$$E=mc^2$$ $$f(x) = x^2$$ $$\alpha = \sqrt{1-e^2}$$ $$\(\sqrt{3x-1}+(1+x)^2\)$$

解析为：

E=mc^2

f(x) = x^2

\alpha = \sqrt{1-e^2}

(\sqrt{3x-1}+(1+x)^2)

3. 多行公式

插入代码块，语言位置填写：

```math 或者 ```latex 或者 ```katex

几个例子：

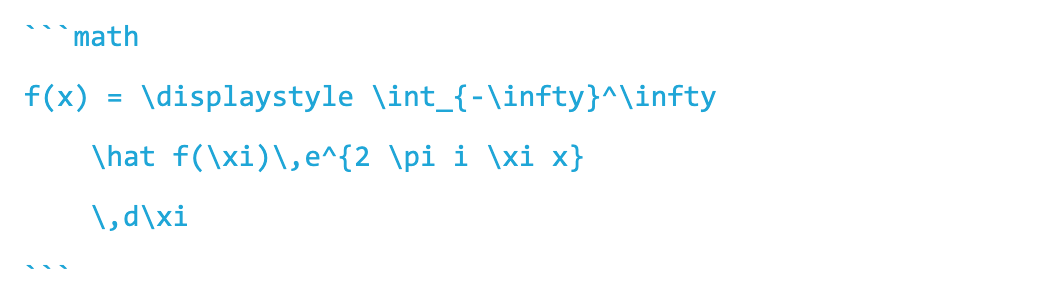
会输出：

f(x) = \displaystyle \int_{-\infty}^\infty \hat f(\xi)\,e^{2 \pi i \xi x} \,d\xi

输出：

\displaystyle \left( \sum_{k=1}^n a_k b_k \right)^2 \leq \left( \sum\limits_{k=1}^n a_k^2 \right) \left( \sum\limits_{k=1}^n b_k^2 \right)

\displaystyle \frac{1}{ \Bigl(\sqrt{\phi \sqrt{5}}-\phi\Bigr) e^{ \frac25 \pi}} = 1+\frac{e^{-2\pi}} {1+\frac{e^{-4\pi}} { 1+\frac{e^{-6\pi}} {1+\frac{e^{-8\pi}} {1+\cdots} } } }

输出：

\displaystyle f(x) = \int_{-\infty}^\infty \hat f(\xi)\,e^{2 \pi i \xi x} \,d\xi

附录：函数渲染参考： $$c = \\pm\\sqrt{a^2 + b^2}$$ $$x > y$$ $$f(x) = x^2$$ $$\alpha = \sqrt{1-e^2}$$ $$\(\sqrt{3x-1}+(1+x)^2\)$$ $$\sin(\alpha)^{\theta}=\sum\limits_{i=0}^{n}(x^i + \cos(f))$$ $$\\dfrac{-b \\pm \\sqrt{b^2 - 4ac}}{2a}$$ $$f(x) = \displaystyle \int_{-\infty}^\infty\hat f(\xi)\,e^{2 \pi i \xi x}\,d\xi$$ $$\displaystyle \frac{1}{\Bigl(\sqrt{\phi \sqrt{5}}-\phi\Bigr) e^{\frac25 \pi}} = 1+\frac{e^{-2\pi}} {1+\frac{e^{-4\pi}} {1+\frac{e^{-6\pi}} {1+\frac{e^{-8\pi}} {1+\cdots} } } }$$ $$\displaystyle \left( \sum\_{k=1}^n a\_k b\_k \right)^2 \leq \left( \sum\_{k=1}^n a\_k^2 \right) \left( \sum\_{k=1}^n b\_k^2 \right)$$ $$a^2$$ $$a^{2+2}$$ $$a_2$$ $${x_2}^3$$ $$x_2^3$$ $$10^{10^{8}}$$ $$a_{i,j}$$ $$_nP_k$$ $$c = \pm\sqrt{a^2 + b^2}$$ $$\frac{1}{2}=0.5$$ $$\dfrac{k}{k-1} = 0.5$$ $$\dbinom{n}{k} \binom{n}{k}$$ $$\displaystyle \oint_C x^3\, dx + 4y^2\, dy$$ $$\displaystyle \bigcap_1^n p \bigcup_1^k p$$ $$e^{i \pi} + 1 = 0$$ $$\displaystyle \left ( \frac{1}{2} \right )$$ $$\displaystyle x_{1,2}=\frac{-b\pm\sqrt{\color{Red}b^2-4ac}}{2a}$$ $${\color{Blue}x^2}+{\color{YellowOrange}2x}-{\color{OliveGreen}1}$$ $$\textstyle \displaystyle \sum_{k=1}^N k^2$$ $$\dfrac{ \tfrac{1}{2}[1-(\tfrac{1}{2})^n] }{ 1-\tfrac{1}{2} } = s_n$$ $$\displaystyle \binom{n}{k}$$ $$0+1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20+\cdots$$ $$\displaystyle \sum_{k=1}^N k^2$$ $$\textstyle \sum_{k=1}^N k^2$$ $$\displaystyle \prod_{i=1}^N x_i$$ $$\textstyle \prod_{i=1}^N x_i$$ $$\displaystyle \coprod_{i=1}^N x_i$$ $$\textstyle \coprod_{i=1}^N x_i$$ $$\displaystyle \int_{1}^{3}\frac{e^3/x}{x^2}\, dx$$ $$\displaystyle \int_C x^3\, dx + 4y^2\, dy$$ $${}_1^2\!\Omega_3^4$$

输出：

c = \pm\sqrt{a^2 + b^2}

x > y

f(x) = x^2

\alpha = \sqrt{1-e^2}

(\sqrt{3x-1}+(1+x)^2)

\sin(\alpha)^{\theta}=\sum\limits_{i=0}^{n}(x^i + \cos(f))

\dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}

f(x) = \displaystyle \int_{-\infty}^\infty\hat f(\xi),e^{2 \pi i \xi x},d\xi

\displaystyle \frac{1}{\Bigl(\sqrt{\phi \sqrt{5}}-\phi\Bigr) e^{\frac25 \pi}} = 1+\frac{e^{-2\pi}} {1+\frac{e^{-4\pi}} {1+\frac{e^{-6\pi}} {1+\frac{e^{-8\pi}} {1+\cdots} } } }

\displaystyle \left( \sum_{k=1}^n a_k b_k \right)^2 \leq \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right)

a^2

a^{2+2}

a_2

{x_2}^3

x_2^3

10^{10^{8}}

a_{i,j}

_nP_k

c = \pm\sqrt{a^2 + b^2}

\frac{1}{2}=0.5

\dfrac{k}{k-1} = 0.5

\dbinom{n}{k} \binom{n}{k}

\displaystyle \oint_C x^3, dx + 4y^2, dy

\displaystyle \bigcap_1^n p \bigcup_1^k p

e^{i \pi} + 1 = 0

\displaystyle \left ( \frac{1}{2} \right )

\displaystyle x_{1,2}=\frac{-b\pm\sqrt{\color{Red}b^2-4ac}}{2a}

{\color{Blue}x^2}+{\color{YellowOrange}2x}-{\color{OliveGreen}1}

\textstyle \displaystyle \sum_{k=1}^N k^2

\dfrac{ \tfrac{1}{2}[1-(\tfrac{1}{2})^n] }{ 1-\tfrac{1}{2} } = s_n

\displaystyle \binom{n}{k}

0+1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20+\cdots

\displaystyle \sum_{k=1}^N k^2

\textstyle \sum_{k=1}^N k^2

\displaystyle \prod_{i=1}^N x_i

\textstyle \prod_{i=1}^N x_i

\displaystyle \coprod_{i=1}^N x_i

\textstyle \coprod_{i=1}^N x_i

\displaystyle \int_{1}^{3}\frac{e^3/x}{x^2}, dx

\displaystyle \int_C x^3, dx + 4y^2, dy

{}_1^2!\Omega_3^4

支持函数

• 全部支持的数学公式请参考 katex.org/docs/supported.html